Sequence and Number Pattern

 A Sequence is a set of things (usually numbers) that are in order.

Each number in the sequence is called a term (or sometimes "element" or "member"):

Finding Missing Numbers

To find a missing number, first find a Rule behind the Sequence.

Sometimes we can just look at the numbers and see a pattern:

Example: 1, 4, 9, 16, ?

Answer: they are Squares (1²=1, 2²=4, 3²=9, 4²=16, ...)

Rule: x_n = n²

Sequence: 1, 4, 9, 16, 25, 36, 49, ...

Did you see how we wrote that rule using "x" and "n" ?

x_n means "term number n", so term 3 is written x₃

And we also used "n" in the formula, so the formula for term 3 is 3² = 9. This could be written

x₃ = 3² = 9

Once we have a Rule we can use it to find any term. For example, the 25th term can be found by "plugging in" 25 wherever n is.

x₂₅ = 25² = 625

How about another example:

Example: 3, 5, 8, 13, 21, ?

After 3 and 5 all the rest are the sum of the two numbers before, that is 3 + 5 = 8, 5 + 8 = 13 and so on (it is actually part of the Fibonacci Sequence):

Rule: x_n = x_n-1 + x_n-2

Sequence: 3, 5, 8, 13, 21, 34, 55, 89, ...

Now what does x_n-1 mean? It just means "the previous term" because the term number (n) is 1 less (n-1).

So, if n was 6, then x_n = x₆ (the 6th term) and x_n-1 = x_6-1 = x₅ (the 5th term)

So, let's apply that Rule to the 6th term:

x₆ = x_6-1 + x_6-2

x₆ = x₅ + x₄

We already know the 4th term is 13, and the 5th is 21, so the answer is:

x₆ = 21 + 13 = 34

Pretty simple ... just put numbers instead of "n"

Many Rules

One of the troubles with finding "the next number" in a sequence is that mathematics is so powerful we can find more than one Rule that works.

What is the next number in the sequence 1, 2, 4, 7, ?

Here are three solutions (there can be more!):

Solution 1: Add 1, then add 2, 3, 4, ...

So, 1+1=2, 2+2=4, 4+3=7, 7+4=11, etc...

Rule: x_n = n(n-1)/2 + 1

Sequence: 1, 2, 4, 7, 11, 16, 22, ...

(That rule looks a bit complicated, but it works)

Solution 2: After 1 and 2, add the two previous numbers, plus 1:

Rule: x_n = x_n-1 + x_n-2 + 1

Sequence: 1, 2, 4, 7, 12, 20, 33, ...

Solution 3: After 1, 2 and 4, add the three previous numbers

Rule: x_n = x_n-1 + x_n-2 + x_n-3

Sequence: 1, 2, 4, 7, 13, 24, 44, ...

So, we have three perfectly reasonable solutions, and they create totally different sequences.

Which is right? They are all right.

Simplest Rule

When in doubt choose the simplest rule that makes sense, but also mention that there are other solutions.

Finding Differences

Sometimes it helps to find the differences between each pair of numbers ... this can often reveal an underlying pattern.

Here is a simple case:

The differences are always 2, so we can guess that "2n" is part of the answer.

Let us try 2n:

n:	1	2	3	4	5
Terms (xn):	7	9	11	13	15
2n:	2	4	6	8	10
Wrong by:	5	5	5	5	5

The last row shows that we are always wrong by 5, so just add 5 and we are done:

Rule: x_n = 2n + 5

OK, we could have worked out "2n+5" by just playing around with the numbers a bit, but we want asystematic way to do it, for when the sequences get more complicated.

Second Differences

In the sequence {1, 2, 4, 7, 11, 16, 22, ...} we need to find the differences ...

... and then find the differences of those (called second differences), like this:

The second differences in this case are 1.

With second differences we multiply by "n² / 2".

In our case the difference is 1, so let us try n² / 2:

n:	1	2	3	4	5
Terms (xn):	1	2	4	7	11
n2:	1	4	9	16	25
n2 / 2:	0.5	2	4.5	8	12.5
Wrong by:	0.5	0	-0.5	-1	-1.5

We are close, but seem to be drifting by 0.5, so let us try: n² / 2 - n/2

n2 / 2 - n/2:	0	1	3	6	10
Wrong by:	1	1	1	1	1

Wrong by 1 now, so let us add 1:

n2 / 2 - n/2 + 1:	1	2	4	7	11
Wrong by:	0	0	0	0	0

The formula n² / 2 - n/2 + 1 can be simplified to n(n-1)/2 + 1

So by "trial-and-error" we discovered a rule that works:

Rule: x_n = n(n-1)/2 + 1

Sequence: 1, 2, 4, 7, 11, 16, 22, 29, 37, ...

Number Pattern

A list of numbers that follow a certain sequence or pattern.


Example: 1, 4, 7, 10, 13, 16, ... starts at 1 and jumps 3 every time.

Another Example: 2, 4, 8, 16, 32, ... doubles each time

Arithmetic Sequences

An Arithmetic Sequence is made by adding the same value each time.

Example:

1, 4, 7, 10, 13, 16, 19, 22, 25, ...

This sequence has a difference of 3 between each number.
The pattern is continued by adding 3 to the last number each time, like this:

Example:

3, 8, 13, 18, 23, 28, 33, 38, ...

This sequence has a difference of 5 between each number.
The pattern is continued by adding 5 to the last number each time, like this

The value added each time is called the "common difference"

What is the common difference in this example?

19, 27, 35, 43, ...

Answer: The common difference is 8

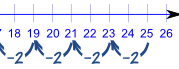
The common difference could also be negative:

Example:

25, 23, 21, 19, 17, 15, ...

This common difference is −2
The pattern is continued by subtracting 2 each time, like this:

Geometric Sequences

A Geometric Sequence is made by multiplying by the same value each time.

Example:

1, 3, 9, 27, 81, 243, ...

This sequence has a factor of 3 between each number.
The pattern is continued by multiplying by 3 each time, like this:

What we multiply by each time is called the "common ratio".

In the previous example the common ratio was 3:

We can start with any number:

Example: Common Ratio of 3, But Starting at 2

2, 6, 18, 54, 162, 486, ...

This sequence also has a common ratio of 3, but it starts with 2.

Example:

1, 2, 4, 8, 16, 32, 64, 128, 256, ...

This sequence starts at 1 and has a common ratio of 2.
The pattern is continued by multiplying by 2 each time, like this:

The common ratio can be 1

Example:

10, 5, 2.5, 1.25, 0.625, 0.3125, ...

This sequence starts at 10 and has a common ratio of 0.5 (a half).

The pattern is continued by multiplying by 0.5 each time.

But the common ratio can't be 0, as we get a sequence like 1, 0, 0, 0, 0, 0, 0, ...

QUESTIONS

Question 1

3, 10, 17, 24, 31, 38, ...

What is the next number in the above sequence?

A.      43

B.      44

C.      45

D.      46

Question 2

71, 62, 53, 44, ...

What is the next number in the above sequence?

A.      35

B.      36

C.      37

D.      38

Question 3 

Here is a number pattern. What is the missing value?

3, 6, 12, ?

A.     10

B.      9

C.      12

D.     24